Icosahedron
An icosahedron is a polyhedron with 20 faces. The prefix "icosa" means twenty. When "icosahedron" is used without any qualifiers, we assume that it is a regular icosahedron, which is an icosahedron in which the 20 faces are all equilateral triangles.
What is an icosahedron
An icosahedron is a three-dimensional figure made up of only polygons. One real life icosahedron example is a 20-sided die, also referred to as D20:

The 20-sided die above is an example of a regular icosahedron, since all of its faces are made up of 20 equilateral triangles. An icosahedron shape can also take on a number of different forms. Below are a few other icosahedron examples:
Properties of a regular icosahedron
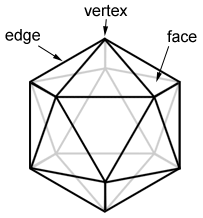
A regular icosahedron is a convex icosahedron whose faces are all congruent regular polygons; specifically, equilateral triangles. Any other type of icosahedron is irregular. The figure below shows three parts that make up an icosahedron: faces, edges, and vertices.
A regular icosahedron is one of 5 Platonic solids, which are types of regular polyhedra. Below are the properties of a regular icosahedron.
- A regular icosahedron has 20 faces, each of which is an equilateral triangle.
- A regular icosahedron has 12 vertices.
- A regular icosahedron has 30 edges.
- 5 faces of a regular icosahedron meet at each vertex.
- Of the 5 platonic solids, the icosahedron has the greatest number of faces.
- Relative to its surface area, an icosahedron has the largest volume of all the platonic solids.
- The angle between the edges of an icosahedron are all 60°, since all its faces are equilateral triangles.
- The dihedral angle of an icosahedron measures approximately 138.19°.
Note that there are other types of icosahedra, such as a rhombic icosahedron, a 19-sided pyramid along with its base, an 18-sided prism and its 2 bases, and more. The other properties of these icosahedra vary, but all have a total of 20 faces, and all are irregular polyhedra.
Surface area of a regular icosahedron
The surface area of a regular icosahedron is the sum of the area of each of its 20 faces. Since each face of a regular icosahedron is an equilateral triangle, its surface area is the area of one of these equilateral triangles multiplied by 20. An equilateral triangle with side length e (which corresponds to the edges of a regular icosahedron) has an area, A, of
The total surface area, S, of a regular icosahedron is therefore:
Volume of a regular icosahedron
The volume, V, of a regular icosahedron is
where e is the length of the edge.
Example:
If the total surface area of a regular icosahedron is , what is its volume?
We can find e by substituting the given value in for the total surface area to get
100 = e2
e = 10
Substituting the length of the edge into the volume formula:
