3D
A three-dimensional space (3D) has three dimensions, such as length, width, and height (or depth). The term "3D" is commonly used to describe shapes and figures in geometry. We live in a 3D world, every object we touch, see, and use are 3D objects. The box, tube, and basketball shown below are just a few examples.

3D shapes and figures
While the dimensions of a 2D shape can be described with length and width, a 3D shape requires an additional dimension, often referred to as height or depth.
| 2D | 3D |
|---|---|
 |  |
| The dimensions of the 2D rectangle above are length and width. | The base of the 3D rectangular prism above is a rectangle that gives it two of its dimensions. The height of the prism is perpendicular to its base giving the prism its third dimension. |
Properties of 3D shapes
3D shapes are characterized by their number of faces, edges, and vertices.
- Faces - A 3D shape's face is one of the 2D sides of the shape. For example, the face of a cube is one of the 6 squares that form the cube. A sphere has 0 faces because it is a curved 3D shape.
- Edges - An edge occurs where 2 faces of a 3D shape meet. For example, a cube has 12 edges, while a sphere has 0.
- Vertices - A vertex occurs where edges meet. A cube has 8 vertices each of which is formed by 3 edges.
Cuboid
A cuboid, also referred to as a 3D rectangle, is a 3D shape with 6 faces. If the edge lengths of the cuboid are all the same, then the cuboid is a cube.

A cuboid is characterized by the following:
- Faces - 6
- Edges - 12
- Vertices - 8
Dimensions of a 3D rectangle
A 3D rectangle has 3 dimensions: length, width, and height (or depth). Typically, the length is the measure of the longest edge, and the width and height (depth) are the other two edges.
Cylinder
A cylinder is a 3D shape made up of two parallel circular bases a fixed distance apart that are joined by a curved surface:

A cylinder is characterized by the following:
- Faces - 2 faces and 1 curved surface
- Edges - 0
- Vertices - 0
Cone
A cone is a 3D shape with a flat circular base that narrows smoothly to a point called the apex, forming an axis to the center of the base:

A cone is characterized by the following:
- Faces - 1 face and 1 curved surface
- Edges - 0
- Vertices - 0
Pyramid

A pyramid is characterized by the following:
- Faces - 4
- Edges - 6 (triangular pyramid) or 8 (rectangular pyramid)
- Vertices - 4 (triangular pyramid) or 5 (rectangular pyramid)
3D Coordinate geometry
Determining the position of a point in 3D is similar to determining the position of a point in 2D, except that there is a third axis, the z-axis, in addition to the x- and y-axes. All three axes are perpendicular to each other, as shown in the figure below.
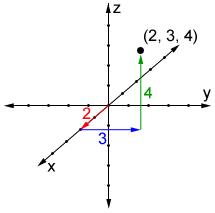
While the x- and y-axes in 2D are conventionally the horizontal and vertical axes, respectively, in 3D their orientations can vary. As such, when determining which direction to move along any axis, the negative and positive direction must be indicated on the axes, as in the image above. A negative value indicates movement along an axis in the negative direction, and a positive value indicates movement in the positive direction. As such, the point (2, 3, 4) indicates movement in the positive direction along each axis in the coordinate space above.
