Volume of a pyramid
The volume of a pyramid is the amount of space it encloses. Below are a few examples of different types of pyramids.
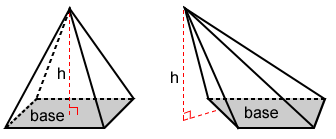
Formula for the volume of a pyramid
The volume, V, of a pyramid is:
where B is the area of the base and h is the height.
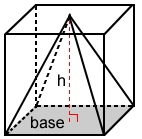
The volume of a prism is Bh. The volume of a pyramid that has the same base and height as the prism it is inscribed in is exactly one-third the volume of the prism. This is true for any pyramid that can be inscribed in a prism as long as the base and height are the same.
Volume of a frustum pyramid
If a plane cuts through a pyramid that is parallel to its base, a frustum is created.
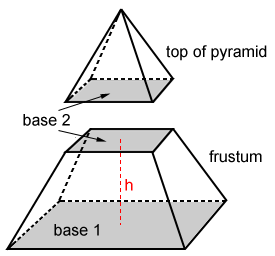
A plane parallel to its base intersects the pyramid above, forming a smaller pyramid above, and a frustum below.
The volume formula for the frustum of a pyramid is
where h is the height of the frustum and A1 and A2 are the areas of the bottom and top bases.
Example:
A frustum is created from a right square pyramid. The height of the frustum is 3, and the two bases have side lengths of 5 and 7 respectively. What is the volume of the frustum?
The areas of the square bases are:
A1 = 72 = 49
A2 = 52 = 25
Using the volume formula above:
| V = | |
| = | |
| = | 74 + 35 |
| = | 109 |
