Volume of a sphere

The volume of a sphere is the amount of space it encloses. A soccer ball is an example of a common spherical object. Its volume is the amount of air it can contain.

Formula for the volume of a sphere

The volume, V, of a sphere with radius r is

The formula for the volume of a sphere can be derived using the formula for the surface area of a sphere, which is 4πr², using a method that approximates the surface area of a sphere using square pyramids.

Let the inside of a sphere of radius r be composed of n square pyramids, each with a height of r and a base with an area of A. The apex of each pyramid is at the center of the sphere, as shown below.

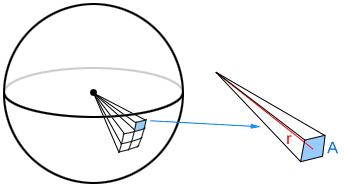
The volume of a pyramid is , where b is the area of the base and h is the height. In the figure above, the volume of each pyramid is therefore . The volume of the sphere can be approximated using the sum of the volumes of n pyramids, as shown in the figure, using the following formula:

The surface area of the sphere can be approximated using the bases of the square pyramids, as nA, where A is the area of each base of the square pyramids used to approximate the sphere, and n is the total number of pyramids used to approximate the sphere. Given that the formula for the surface area of a sphere is 4πr²,

nA ≈ 4πr²

The smaller the bases of the pyramids used to approximate the sphere, the more accurate the approximation, and the larger the number of pyramids, n, we would need to use to approximate the sphere. If an infinite number of pyramids could be composed to create the exact volume of the sphere, then

nA = 4πr²

Substituting this into the approximate volume formula, we can find the volume of a sphere in terms of π:

Volume of a hemisphere

In geometry, a hemisphere is created by a plane intersecting a sphere through its center.

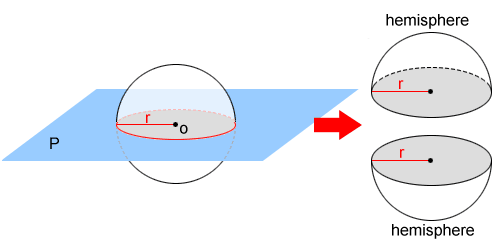
In the figure above, plane P intersects sphere O through its center, creating two hemispheres of equal size. Since a hemisphere is half of a sphere, the volume of a hemisphere is:

where r is the radius of the hemisphere.