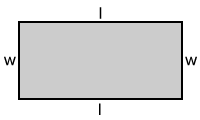
Perimeter of a rectangle
The perimeter of a rectangle is the sum of the lengths of all of its sides:
P = 2l + 2w
where P is perimeter, l is length, and w is width.
Example:
Find the perimeter of the tennis court with a length of 78 feet and width of 27 feet.
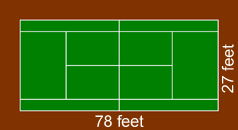
| P = | 2l + 2w |
| = | 2 × 78 + 2 × 27 |
| = | 210 feet |
Example:
Find the perimeter of rectangle whose length is twice the size of its width, and has a diagonal of 10.
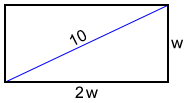
The diagonal divides the rectangle into two congruent right triangles. Using the Pythagorean theorem, we can find w:
w2 + (2w)2 = 102
w2 = 20
w = 2
| P = | 2l + 2w |
| = | 2(2w) + 2w |
| = | 6w |
| = | |
| = |
