Line segment
A line segment is a part of a line defined by two endpoints. A line segment consists of all points on the line between (and including) said endpoints.
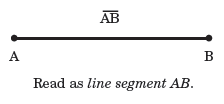
Line segments are often indicated by a bar over the letters that constitute each point of the line segment, as shown above.
Dividing a line segment
A point that lies in the interior of a line segment divides the segment into 2 segments.

In the segment above, point C divides into and , AC + CB = AB. This is known as the segment addition postulate.
The midpoint of a line segment is a point that divides the segment into 2 congruent segments.
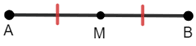
In the figure above, point M is the midpoint of so, ≅.
Line segments through midpoints.
A segment is a bisector of another segment if it goes through the midpoint of the segment.
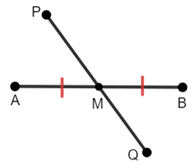
A segment is called a perpendicular bisector of another segment if it goes through the midpoint and is perpendicular to the segment.
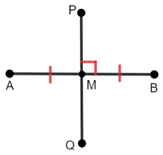
While there can be many segments that bisect another segment, only one segment can be the perpendicular bisector.
Line segments and polygons
The sides of a polygon are line segments. A polygon is an enclosed plane figure whose sides are line segments.
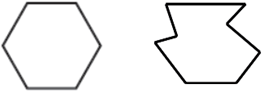
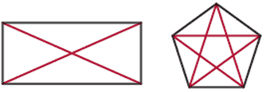
A diagonal for a polygon is a line segment joining two non-consecutive vertices (not next to each other).
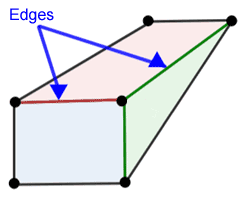
Line segments and polyhedrons
Edges formed by the intersection of two faces of a polyhedron are line segments. It takes three or more-line segments forming edges to enclose a face of a polyhedron.